Visualización 3D usando OpenGL
Las matrices son ampliamente utilizadas en la visualización de gráficos 3D, OpenGL las utiliza para aplicar transformaciones (escalado, traslación, rotación) a los objetos 3D, manipular la vista de proyección, entre otras cosas, para empezar veremos cómo mostrar un objeto tridimensional en pantalla (el clásico cubo).
Define lo que estará visible en pantalla, OpenGL soporte dos tipos de proyección, perspectiva y ortográfica, usaremos la primera ya que nos proporciona un resultado realista, parecido al mundo real, la proyección ortográfica es usada comúnmente en programas CAD.
Para la creación de la matriz de proyección en perspectiva utilizaremos la función GLM perspective(fovy, aspect, zNear, zFar), fovy define el ángulo de visión, aspect la relación (ancho/alto) de la pantalla, zNear y zFar son las distancias de los planos de recorte.
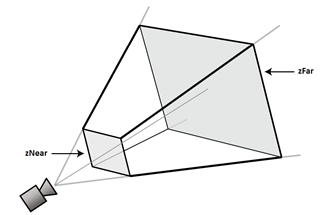
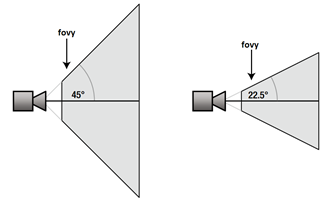
Ha esto se le llama pirámide de visualización, todo lo que se encuentre dentro del área marcada será lo que podremos visualizar en pantalla, en la figura inferior vemos como el cambio de ángulo de visión afecta la pirámide.
Esta matriz indica la ubicación de la cámara, a donde mira la misma y su orientación, la creamos mediante la función GLM lookAt(eye, center, up), donde eye es el punto donde se ubica la cámara, center es donde mira la cámara y up define el vector vertical.

En este punto hemos definido la cámara, donde se ubica, hacia donde mira y el rango de visualización de la misma, todo lo hemos hecho utilizando matrices, la librería GLM no proporciona mat4, una matriz de 4x4 y las funciones para la creación y manipulación de estas matrices.
Partiendo del tutorial anterior donde dibujamos un triángulo 2D haremos las siguientes modificaciones para agregar los 8 vértices necesarios para generar un cubo, agregamos también los índices necesarios para dibujar el cubo, recordemos que un índice especifica como se unen los vértices para formar una determinada figura.
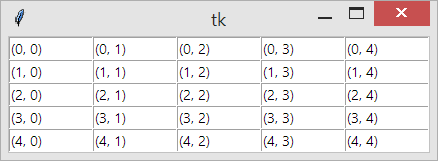
El primer triangulo será dibujado usando los vértices indicados por los índices (0, 1, 2), el segundo usando los 3 vértices indicados por los siguientes índices (7, 6, 5), seguimos de este modo hasta dibujar los 12 triángulos que requiere un cubo.
Al igual que los vértices, los índices también deben ser almacenados en un buffer, el procedimiento es el mismo, puedes ir el tutorial anterior para más detalles, solo cambia el tipo a GL_ELEMENT_ARRAY_BUFFER.
En el tutorial anterior vimos como pasar datos de vértices a los shaders, ahora requerimos enviar las matrices al shader para que el mismo aplique las correspondientes transformaciones, antes usamos un tipo de variable en los shader llamada attribute que usamos para manipular los buffer de color y vertices, ahora usaremos uniform a diferencia del attribute este retiene su valor en cada ejecución del shader.
Modificamos el vertex shader para recibir la matriz correspondiente a las transformaciones y lo multiplicamos por cada vértice en el buffer.
Para enviar la matriz al shader usaremos glUniformMatrix4fv(MatrixID, 1, GL_FALSE, &MVP[0][0]).
Podemos usar la multiplicación de matrices para crear una matriz total, esta contiene la matriz de proyección, la matriz de visualización y la matriz de modelo, pudimos pasarlas individualmente al shader y luego multiplicarlas, pero, la primera forma es más eficiente.
La matriz de modelo en esta caso llamada: Model, es la que contiene las transformaciones del modelo como: rotación, traslación y escalado, en este ejemplo aplicamos una rotación para hacer girar el cubo sobre el eje Y, más adelante veremos en detalle las transformaciones.

GitHub: Visualización 3D OpenGL
Transformación de proyección
Define lo que estará visible en pantalla, OpenGL soporte dos tipos de proyección, perspectiva y ortográfica, usaremos la primera ya que nos proporciona un resultado realista, parecido al mundo real, la proyección ortográfica es usada comúnmente en programas CAD.
Para la creación de la matriz de proyección en perspectiva utilizaremos la función GLM perspective(fovy, aspect, zNear, zFar), fovy define el ángulo de visión, aspect la relación (ancho/alto) de la pantalla, zNear y zFar son las distancias de los planos de recorte.

Ha esto se le llama pirámide de visualización, todo lo que se encuentre dentro del área marcada será lo que podremos visualizar en pantalla, en la figura inferior vemos como el cambio de ángulo de visión afecta la pirámide.

Transformación de visualización
Esta matriz indica la ubicación de la cámara, a donde mira la misma y su orientación, la creamos mediante la función GLM lookAt(eye, center, up), donde eye es el punto donde se ubica la cámara, center es donde mira la cámara y up define el vector vertical.

En este punto hemos definido la cámara, donde se ubica, hacia donde mira y el rango de visualización de la misma, todo lo hemos hecho utilizando matrices, la librería GLM no proporciona mat4, una matriz de 4x4 y las funciones para la creación y manipulación de estas matrices.
glm::mat4 Projection = glm::perspective(45.0f, 4.0f / 3.0f, 0.1f, 100.0f); glm::mat4 View = glm::lookAt(glm::vec3(4, 3, -3), glm::vec3(0, 0, 0), glm::vec3(0, 1, 0));
Dibujar Cubo Usando Índices
Partiendo del tutorial anterior donde dibujamos un triángulo 2D haremos las siguientes modificaciones para agregar los 8 vértices necesarios para generar un cubo, agregamos también los índices necesarios para dibujar el cubo, recordemos que un índice especifica como se unen los vértices para formar una determinada figura.
// vetices para generar un cubo 3D static const float vertex[] = { 1.0f, -1.0f, -1.0f, 1.0f, 1.0f, -1.0f, 1.0f, 1.0f, -1.0f, -1.0f, 1.0f, 1.0f, -1.0f, -1.0f, -1.0f, 1.0f, 1.0f, 1.0f, -1.0f, 1.0f, 1.0f, 1.0f, 1.0f, 1.0f, -1.0f, 1.0f, 1.0f, 1.0f, -1.0f, 1.0f, -1.0f, 1.0f }; // componetes RGBA para los colores de cada vertice static const float color[] = { /.../ }; // indices usados para unir los vertices que componen el cubo static const GLushort indices[] = { 0, 1, 2, 7, 6, 5, 4, 5, 1, 5, 6, 2, 6, 7, 3, 0, 3, 7, 3, 0, 2, 4, 7, 5, 0, 4, 1, 1, 5, 2, 2, 6, 3, 4, 0, 7 }; // generar, almacenar el buffer de indices glGenBuffers(1, &index_buffer); glBindBuffer(GL_ELEMENT_ARRAY_BUFFER, index_buffer); glBufferData(GL_ELEMENT_ARRAY_BUFFER, sizeof(indices), indices, GL_STATIC_DRAW);
El primer triangulo será dibujado usando los vértices indicados por los índices (0, 1, 2), el segundo usando los 3 vértices indicados por los siguientes índices (7, 6, 5), seguimos de este modo hasta dibujar los 12 triángulos que requiere un cubo.
Al igual que los vértices, los índices también deben ser almacenados en un buffer, el procedimiento es el mismo, puedes ir el tutorial anterior para más detalles, solo cambia el tipo a GL_ELEMENT_ARRAY_BUFFER.
Uso de uniform en shader
En el tutorial anterior vimos como pasar datos de vértices a los shaders, ahora requerimos enviar las matrices al shader para que el mismo aplique las correspondientes transformaciones, antes usamos un tipo de variable en los shader llamada attribute que usamos para manipular los buffer de color y vertices, ahora usaremos uniform a diferencia del attribute este retiene su valor en cada ejecución del shader.
Modificamos el vertex shader para recibir la matriz correspondiente a las transformaciones y lo multiplicamos por cada vértice en el buffer.
layout (location = 0) in vec4 vPosition; layout (location = 1) in vec4 vColor; uniform mat4 MVP; out vec4 color; void main(void) { gl_Position = MVP * vPosition; color = vColor; }
Para enviar la matriz al shader usaremos glUniformMatrix4fv(MatrixID, 1, GL_FALSE, &MVP[0][0]).
Podemos usar la multiplicación de matrices para crear una matriz total, esta contiene la matriz de proyección, la matriz de visualización y la matriz de modelo, pudimos pasarlas individualmente al shader y luego multiplicarlas, pero, la primera forma es más eficiente.
void onrender(double time) override { glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT); glEnable(GL_CULL_FACE); shader_simple.use(); glm::mat4 Model = glm::rotate(glm::mat4(1.0f), (float)time, glm::vec3(0.0f, 1.0f, 0.0f)); glm::mat4 Projection = glm::perspective(45.0f, aspect_ratio, 0.1f, 100.0f); glm::mat4 View = glm::lookAt(glm::vec3(4, 3, -3), glm::vec3(0, 0, 0), glm::vec3(0, 1, 0)); glm::mat4 MVP = Projection * View * Model; // Enviar las tranformaciones al shader // MatrixID es el ID del uniform MVP obtenida por glGetUniformLocation(program, "MVP"); glUniformMatrix4fv(MatrixID, 1, GL_FALSE, &MVP[0][0]); // Dibujar cubo usando los indices almacenados en el buffer, // 1 triangulo = 3 indices, 1 cara = 2 triangulos, 1 cubo = 6 caras. // 3 * 2 * 6 = 36 indices a dibujar glDrawElements(GL_TRIANGLES, 36, GL_UNSIGNED_SHORT, 0); }
La matriz de modelo en esta caso llamada: Model, es la que contiene las transformaciones del modelo como: rotación, traslación y escalado, en este ejemplo aplicamos una rotación para hacer girar el cubo sobre el eje Y, más adelante veremos en detalle las transformaciones.

GitHub: Visualización 3D OpenGL



Comentarios
Publicar un comentario