Modelo de Iluminación Phong - Tutorial OpenGL
En la programación de gráficos 3D existen distintos modelos de iluminación que intentan simular cómo se comporta la luz al iluminar la superficie de un objeto tridimensional, uno de esto es el modelo de iluminación Phong, lo podemos aplicar por vértice (Gouraud shading) o por pixel (Phong shading).
El modelo de iluminación phong utiliza tres componentes básicos:

Ecuación para el cálculo de la iluminación en un punto:
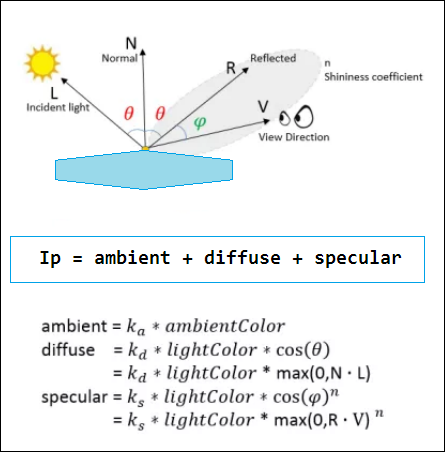
Esta fórmula utiliza los vectores: L, N, R, V, y las constantes: Ka, Kd, Ks, que se definen como:
Esta técnica calcula la iluminación para cada vértice e interpola el resultado entre los vértices, esta técnica implemente todo el código en el vertex shader.
Para calcular los vectores mencionados requerimos enviar las matrices vista-modelo, vista y proyección al vertex shader, también requerimos tener a mano los vectores normales, usaremos como base el código del tutorial OpenGL (Cargar Modelo 3D OBJ) este obtiene la información de vértices, textura y normales de un archivo obj.
Las 3 primeras variables (position, texture, normal) de tipo in (entrada) son enviadas a través de los correspondientes buffer, para este ejemplo no utilizaremos las texturas.
Las siguientes 3 variables (mv_matrix, view_matrix, proj_matrix) de tipo uniform mat4 son las matrices de vista-modelo, vista y proyección respectivamente, para enviar estas matrices al shader debemos obtener su localizador para luego modificar su valor, de la siguiente manera:
El resto de las variables son las requeridas para el cálculo de la ecuación de iluminación, son de tipo uniform por lo que podemos establecer su valor desde código C++ como lo hicimos con las matrices, para simplificar establecemos un valor inicial.
Lo siguiente es el resto del vertex shader, calculamos los correspondientes vectores y aplicamos la formula, nos apoyamos en las funciones GLSL: normalize (para normalizar el vector), max (obtener el máximo de dos valores), pow (elevar a una potencia), reflect (calcula el vector reflejado).
En el fragment shader solo aplicaremos el color recibido desde el vertex shader, que es la suma de las componentes, ambiente, difusa y especular.

Esta técnica utiliza la misma fórmula antes mencionada, salvo que calcularemos la intensidad de luz para cada pixel, por lo que dividimos la formula en dos partes, en el vertex shader calculamos los vectores: N, V, L, los pasamos al fragmente shader para calcular la intensidad de luz en cada pixel.
Nuestro Vertex Shader (Modelo de Iluminación Phong)
En el fragment shader calculamos el color final, veamos nuestro Fragment Shader para el Modelo de Iluminación Phong.
Ejecutamos el código ahora con el nuevo shader, en el proyecto en github se incluyen ambos shader, para probarlos basta solo con cambiar el nombre del shader que deseamos usar.
En la siguiente imagen se muestra la diferencia entre Phong y Gouraud shading, esta diferencia puede ser difícil de percibir sobre alguna superficies, sobre todo las planas como un cubo.

Mostramos otra imagen donde se ve cómo es la salida al cambiar el valor n (Coeficiente de brillo), este valor normalmente se encuentra entre 0 y 128, entre más grande es, más pequeño es el efecto de brillo.

Para entender cómo afecta el cambio de cada uno de los valor que intervienen en la ecuación es lo más fácil es hacer el cambio y ver la salida, podríamos modificar la aplicación para hacer los cambios y verlos en tiempo real mientras se ejecuta la aplicación, pero eso será para la próxima.
GitHub: Modelo de Iluminación Phong
El modelo de iluminación phong utiliza tres componentes básicos:
- Ambiente: La luz que llega rebotada de las paredes, los muebles, etc., se refleja en todas las direcciones simultáneamente.
- Difusa: La luz que llega directamente desde la fuente de luz pero rebota en todas direcciones, combinada con la luz ambiental definen el color del objeto.
- Especular: La luz que llega directamente de la fuente de luz y rebota en una dirección, según la normal de la superficie. Es la que afecta al "brillo" de la superficie.

Ecuación para el cálculo de la iluminación en un punto:

Esta fórmula utiliza los vectores: L, N, R, V, y las constantes: Ka, Kd, Ks, que se definen como:
- L: Vector del punto a la luz.
- N: Normal en el punto.
- R: Vector reflejado (L reflejado sobre N).
- V: Vector del punto al centro de la cámara.
- Ka: Factor de luz ambiente del objeto.
- Kd: Factor de luz difusa del objeto.
- Ks: Factor de luz especular del objeto.
- n: Coeficiente de brillo (Shinniness coefficient).
Gouraud Shading
Esta técnica calcula la iluminación para cada vértice e interpola el resultado entre los vértices, esta técnica implemente todo el código en el vertex shader.
Para calcular los vectores mencionados requerimos enviar las matrices vista-modelo, vista y proyección al vertex shader, también requerimos tener a mano los vectores normales, usaremos como base el código del tutorial OpenGL (Cargar Modelo 3D OBJ) este obtiene la información de vértices, textura y normales de un archivo obj.
layout (location = 0) in vec4 position; layout (location = 1) in vec2 texture; layout (location = 2) in vec3 normal; uniform mat4 mv_matrix; uniform mat4 view_matrix; uniform mat4 proj_matrix; uniform vec3 light_pos = vec3(100.0, 100.0, 100.0); uniform vec3 light_color = vec3(0.75, 0.75, 0.75); uniform vec3 ambient_color = vec3(0.0); uniform float ka = 0.00; uniform float kd = 0.70; uniform float ks = 0.35; uniform int n = 32; out vec3 color;
Las 3 primeras variables (position, texture, normal) de tipo in (entrada) son enviadas a través de los correspondientes buffer, para este ejemplo no utilizaremos las texturas.
loadOBJ("model/cubo.obj", vertex, normal, uv); // generar dos ids para los buffer glGenBuffers(3, buffer); // buffer de vertices glBindBuffer(GL_ARRAY_BUFFER, buffer[0]); glBufferData(GL_ARRAY_BUFFER, vertex.size() * sizeof(glm::vec3), &vertex[0], GL_STATIC_DRAW); glVertexAttribPointer(0, 3, GL_FLOAT, GL_FALSE, 0, NULL); glEnableVertexAttribArray(0); // buffer de normales glBindBuffer(GL_ARRAY_BUFFER, buffer[2]); glBufferData(GL_ARRAY_BUFFER, normal.size() * sizeof(glm::vec3), &normal[0], GL_STATIC_DRAW); glVertexAttribPointer(2, 3, GL_FLOAT, GL_FALSE, 0, NULL); glEnableVertexAttribArray(2);
Las siguientes 3 variables (mv_matrix, view_matrix, proj_matrix) de tipo uniform mat4 son las matrices de vista-modelo, vista y proyección respectivamente, para enviar estas matrices al shader debemos obtener su localizador para luego modificar su valor, de la siguiente manera:
// crear, compilar y enlasar el Vertex y Fragment Shader GLuint program = shader_simple.compile("shaders/simple.vertex_shader", "shaders/simple.fragment_shader"); mv_matrix = glGetUniformLocation(program, "mv_matrix"); view_matrix = glGetUniformLocation(program, "view_matrix"); proj_matrix = glGetUniformLocation(program, "proj_matrix"); //...// // Matriz de modelo, se aplica una rotacion sobre el eje Y glm::mat4 Model; Model = glm::rotate(Model, (float)time, glm::vec3(0.0f, 1.0f, 0.0f)); // Matriz de proyeccion y visualizacion glm::mat4 Projection = glm::perspective(45.0f, aspect_ratio, 0.1f, 100.0f); glm::mat4 View = glm::lookAt(glm::vec3(4, 3, -3), glm::vec3(0, 0, 0), glm::vec3(0, 1, 0)); glm::mat4 MV = View * Model; // Establecer las matrices glUniformMatrix4fv(mv_matrix, 1, GL_FALSE, &MV[0][0]); glUniformMatrix4fv(view_matrix, 1, GL_FALSE, &View[0][0]); glUniformMatrix4fv(proj_matrix, 1, GL_FALSE, &Projection[0][0]);
El resto de las variables son las requeridas para el cálculo de la ecuación de iluminación, son de tipo uniform por lo que podemos establecer su valor desde código C++ como lo hicimos con las matrices, para simplificar establecemos un valor inicial.
Lo siguiente es el resto del vertex shader, calculamos los correspondientes vectores y aplicamos la formula, nos apoyamos en las funciones GLSL: normalize (para normalizar el vector), max (obtener el máximo de dos valores), pow (elevar a una potencia), reflect (calcula el vector reflejado).
void main() { // Calculate view-space coordinate vec4 P = mv_matrix * position; // Calculate normal in view space vec3 N = normalize(mat3(mv_matrix) * normal); // Calculate view-space light vector vec3 L = normalize(light_pos - P.xyz); // Calculate view vector (simply the negative of the view-space position) vec3 V = normalize(-P.xyz); // Calculate R by reflecting -L around the plane defined by N vec3 R = reflect(-L, N); // Calculate ambient, difusse, specular contribution vec3 ambient = ka * ambient_color; vec3 diffuse = kd * light_color * max(0.0, dot(N, L)); vec3 specular = ks * light_color * pow(max(0.0, dot(R, V)), n); // Send the color output to the fragment shader color = ambient + diffuse + specular; // Calculate the clip-space position of each vertex gl_Position = proj_matrix * P; }
En el fragment shader solo aplicaremos el color recibido desde el vertex shader, que es la suma de las componentes, ambiente, difusa y especular.

Phong shading
Esta técnica utiliza la misma fórmula antes mencionada, salvo que calcularemos la intensidad de luz para cada pixel, por lo que dividimos la formula en dos partes, en el vertex shader calculamos los vectores: N, V, L, los pasamos al fragmente shader para calcular la intensidad de luz en cada pixel.
Nuestro Vertex Shader (Modelo de Iluminación Phong)
layout (location = 0) in vec4 position; layout (location = 1) in vec2 texture; layout (location = 2) in vec3 normal; uniform mat4 mv_matrix; uniform mat4 view_matrix; uniform mat4 proj_matrix; uniform vec3 light_pos = vec3(0.0, 3.0, -3.0); out vec3 N1; out vec3 L1; out vec3 V1; void main(void) { // Calculate view-space coordinate vec4 P = mv_matrix * position; // Calculate normal in view-space N1 = mat3(mv_matrix) * normal; // Calculate light vector L1 = light_pos - P.xyz; // Calculate view vector V1 = -P.xyz; // Calculate the clip-space position of each vertex gl_Position = proj_matrix * P; }
En el fragment shader calculamos el color final, veamos nuestro Fragment Shader para el Modelo de Iluminación Phong.
out vec4 color; in vec3 N1; in vec3 L1; in vec3 V1; uniform vec3 light_color = vec3(0.75, 0.75, 0.75); uniform vec3 ambient_color = vec3(0.1); uniform float ka = 0.10; uniform float kd = 0.55; uniform float ks = 0.70; uniform float n = 32; void main() { // Normalize the incoming N, L, and V vectors vec3 N = normalize(N1); vec3 L = normalize(L1); vec3 V = normalize(V1); // Calculate R by reflecting -L around the plane defined by N vec3 R = reflect(-L, N); // Calculate ambient, difusse, specular contribution vec3 ambient = ka * ambient_color; vec3 diffuse = kd * light_color * max(0.0, dot(N, L)); vec3 specular = ks * light_color * pow(max(0.0, dot(R, V)), n); // Send the color output to the fragment shader vec3 f_color = ambient + diffuse + specular; color = vec4(f_color, 1.0); }
Ejecutamos el código ahora con el nuevo shader, en el proyecto en github se incluyen ambos shader, para probarlos basta solo con cambiar el nombre del shader que deseamos usar.
En la siguiente imagen se muestra la diferencia entre Phong y Gouraud shading, esta diferencia puede ser difícil de percibir sobre alguna superficies, sobre todo las planas como un cubo.

Mostramos otra imagen donde se ve cómo es la salida al cambiar el valor n (Coeficiente de brillo), este valor normalmente se encuentra entre 0 y 128, entre más grande es, más pequeño es el efecto de brillo.

Para entender cómo afecta el cambio de cada uno de los valor que intervienen en la ecuación es lo más fácil es hacer el cambio y ver la salida, podríamos modificar la aplicación para hacer los cambios y verlos en tiempo real mientras se ejecuta la aplicación, pero eso será para la próxima.
GitHub: Modelo de Iluminación Phong



Muchas gracias por su artículo. Me ha ayudado mucho a solucionar un error que no veía. Usaba la misma ecuación que saque del libro de Richard S. Wright y Benjamin Lipchak (con distintos nombres en las variables dentro del Shader) y no encontraba el error en la luz especular, al comparar con su Shader, me dí cuenta de un error muy simple en una resta. Simple, si, pero gracias a su artículo lo he encontrado. Lo correcto es dar las gracias.
ResponderEliminar